Het huidige thuisonderwijs maakt goed zichtbaar dat kinderen tegenwoordig niet op dezelfde manier leren rekenen als hun ouders vroeger. De manier waarop we deelsommen uitrekenen, is hier een goed voorbeeld van. Ouders leerden vroeger de ‘ouderwetse’ staartdeling, kinderen leren het tegenwoordig op een andere manier. De staartdeling is daarmee een icoon van de veranderingen in het rekenonderwijs geworden. Het is dan ook niet verwonderlijk dat juist dit onderdeel van rekenen voor verwarring aan de keukentafel zorgt. Een vader verzucht “Ik heb mijn dochter maar de staartdeling aangeleerd, maar die moet ze misschien later wel weer afleren”. Maar zijn die twee methoden echt zo anders? Waar komt de verandering eigenlijk vandaan? En welke methode is beter?

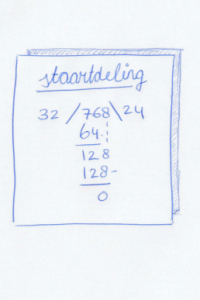
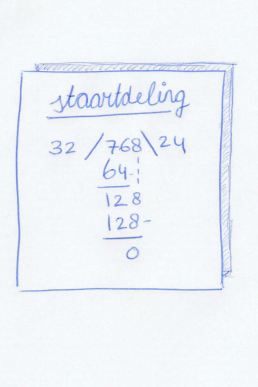
Staartdeling

Ouders herinneren zich waarschijnlijk nog de eindeloze rijen staartdelingen die ze op de basisschool hebben moeten maken. Neem de som 768 : 32 in het voorbeeld. Links beginnen: past 32 in 7? Nee, dus we pakken er nog een cijfertje bij. Past 32 in 76? Ja, 2 x 32 = 64! De 2 schrijven we rechtsboven op als eerste cijfer van de uitkomst, de 64 zetten we onder de 76. Dan trekken we 64 van 76 af, dat geeft 12. Gevolgd door een magische stap: we halen de 8 naar beneden en plakken die aan de 12. Opeens is dit 128 geworden. In 128 past 32 precies 4 keer. 4 opschrijven als tweede cijfer van de uitkomst en voilà: het antwoord is 24.

Heb je het trucje eenmaal onder de knie, dan kan je goede antwoorden blijven produceren. Je bent een algoritme expert! Je volgt een vast stappenplan dat heel efficiënt naar het goede antwoord leidt. Maar begrijp jij echt wat je doet? Waarom wordt bijvoorbeeld de ‘2’ die als eerste cijfer van het antwoord wordt opgeschreven uiteindelijk een 20 en waarom werkt dat naar beneden halen van cijfers uit het deeltal?

Happendelen

Heb jij trouwens ná je schooltijd nog wel eens een staartdeling gemaakt? Als je nu een deelsom moet uitrekenen en je telefoon er niet bij pakt, probeer je waarschijnlijk af te passen: hoe vaak past 32 in 768? Eens kijken..., we beginnen gewoon met 10 x 32 = 320, dat gaat in ieder geval en dan hebben we nog 768 – 320 = 448 over. Hé, daar past 320 nog wel een keer in! Dan hebben we nog 128 over en laat dat nou precies 4 x 32 zijn. In totaal hebben we dus 10 + 10 + 4 = 24 keer het getal 32 afgepast.

Als je die stappen van herhaald aftrekken gestructureerd onder elkaar opschrijft, heb je het zogenoemde 'kolomsgewijs delen,' ook wel bekend als 'happendelen'.

Een belangrijk verschil met de staartdeling zijn de nullen: 768 wordt niet zomaar 76. Daarnaast is er ruimte om zelf de ‘happen’ te kiezen, terwijl je in de staartdeling genadeloos wordt afgestraft als je niet de optimale vermenigvuldiging pakt.

Traditioneel versus realistisch rekenen

De omslag van staartdelingen naar happendelen is een mooie illustratie van de veranderingen in het rekenonderwijs. In het traditionele rekenonderwijs lag de nadruk op het vlot en efficiënt kunnen uitvoeren van rekenprocedures. In het realistische rekenonderwijs, dat sinds de jaren ’70 en ’80 van de vorige eeuw steeds populairder werd, staat centraal dat leerlingen niet alleen goed hun rekenprocedures kunnen uitvoeren, maar vooral ook begrijpen wát ze doen en waarom dát werkt. Daarom worden nieuwe manieren van uitrekenen aangeboden. Deze kolomsgewijze manieren hebben als doel het ‘onder elkaar rekenen’ inzichtelijk aan te leren, in plaats van als losse verzameling rekenstappen waar je niet per se iets van hoeft te begrijpen.

Bij optellen, aftrekken en vermenigvuldigen worden deze kolomsgewijze manieren al snel omgebouwd naar het ‘cijferend’ onder elkaar rekenen. Bij deelsommen ligt dat anders: de staartdeling is een tijd helemaal uit de rekenboeken verdwenen. En hoewel hij weer terug is in de nieuwere versies, wordt hij meestal pas in groep 8 aangeboden en ook niet aan alle leerlingen. De huidige generatie kinderen leert de staartdeling dus vaak niet of nauwelijks.

Welke methode is beter?

Leg je de meest korte vorm van het happendelen - met in het voorbeeld happen van 20 en 4 - naast de staartdeling, dan zie je dat ze eigenlijk maar weinig van elkaar verschillen. Uit onderzoek blijkt dan ook dat de twee manieren ongeveer even goed werken. Het maakt dus niet zoveel uit welke manier kinderen gebruiken. Veel belangrijker is dat kinderen hun rekenstappen op papier zetten: dit helpt in het structureren van de uitwerking en geeft meer ruimte in het werkgeheugen. Verontrustend is dan ook dat kinderen nu vaker dan vroeger dit soort sommen uit het hoofd uitrekenen. En onderzoek toont aan dat dat leidt tot slechtere prestaties.

Dus laten we vooral het gestructureerd opschrijven van de berekening stimuleren, ongeacht de manier van berekening. Ook is het goed mogelijk om de brug te slaan tussen happendelen, als manier die goed werkt en goed te begrijpen is, naar de staartdeling, als de meest efficiënte en korte vorm hiervan.

Hoe verder aan die keukentafel?

Het is dus niet 'óf óf', het kan 'én én' zijn: happendelen én de staartdeling kunnen elkaar juist aanvullen. Laat je kind de stappen van het happendelen opschrijven en uitleggen. “Kijk, als we de nullen weghalen en altijd zoeken naar de grootste hap, dan hebben we de staartdeling!” Zo’n gesprek over hoe verschillende rekenmanieren werken, is een heel effectief leermiddel om begrip en prestaties bij rekenen te bevorderen. Voor kinderen, maar vast ook voor ouders!